1.4二极管特性

在本教程中，我们将学习一些重要的二极管特性。通过研究这些二极管特性，您将更好地理解二极管的工作原理。

常用的二极管特性

• 二极管电流方程
• 直流电阻
• 交流电阻
• 过渡电容
• 扩散电容
• 存储时间
• 过渡时间
• 恢复时间

现在，我们将简要了解一下这些二极管特性。

二极管电流方程

PN 结二极管以其单向导电性而闻名。流过PN 结二极管的电流大小取决于所使用的材料类型以及PN 二极管制造中的掺杂浓度。

电流流动的主要原因是由于PN 结二极管结构中多数载流子的产生或复合。

我们有三个区域负责多数载流子电流的流动。这些区域分别是准中性P区、耗尽区和准中性N区。准中性P区是耗尽区边缘与P侧二极管边缘之间的区域。

准中性N区是耗尽区边缘与N侧二极管边缘之间的区域。假设这种分离距离为无穷大。当我们向二极管的边界移动时，载流子浓度不会发生变化。准中性区中不存在电场。

$\Delta n_p(x \to -\infty) = 0$ $\Delta p_n(x \to +\infty) = 0$

正向偏置下的二极管电流是由于多数载流子的复合。载流子复合发生在P型或N型准中性区、耗尽区或欧姆接触处（即金属与半导体的接触处）。

反向偏置下的电流流动是由于载流子的产生。这种载流子产生过程进一步增加了正向和反向偏置条件下的电流流动。

PN 结二极管中的电流流动由载流子密度、整个PN 结结构中的电场以及P型和N型的准费米能级决定。载流子密度和电场用于确定PN 二极管的漂移电流和扩散电流。

假设耗尽区内的电子和空穴的准费米能级以及N型和P型准中性区内的准费米能级大致相等，以获得解析解。

如果假设费米能级在耗尽区内是恒定的，则耗尽区边界处的少数载流子密度如下：

当没有外部电压施加时，上述方程达到热平衡状态。随着外部施加电压的增加，费米能级之间的分离增大。这个外部电压乘以电子的电荷。

当准中性区中的多余载流子到达金属-半导体接触时，它们会立即复合。复合过程在欧姆接触处迅速发生，并且由于金属的存在而进一步增加。因此，有效的边界条件可以表示为：

$p_n(x = w_n) = p_{n0}$ $n_p(x = -w_p) = n_{p0}$

考虑N型和P型准中性区的扩散电流方程，使用上述边界条件可以得到理想二极管的电流表达式。

将上述方程转换为双曲函数形式，重写为：

$p_n(x \geq x_n) = p_{n0} + A \cosh\left(\frac{x - x_n}{L_p}\right) + B \sinh\left(\frac{x - x_n}{L_p}\right)$ $n_p(x \leq -x_p) = n_{p0} + C \cosh\left(\frac{x + x_p}{L_n}\right) + D \sinh\left(\frac{x + x_p}{L_n}\right)$

其中A、B、C和D是待确定的常数值。如果将边界条件应用于上述双曲方程，则有：

其中N型和P型准中性区的宽度分别为：

$w'_n = w_n - x_n$ $w'_p = w_p - x_p$

每个准中性区中的载流子电流密度由扩散电流方程计算得出。

在整个PN 结二极管结构中流动的电流总量必须保持恒定，因为电荷不能在二极管的整个结构中消失或积累。

因此，通过二极管的总电流等于N区中的最大空穴电流、P区中的最大电子电流以及由于耗尽区中载流子复合而产生的电流之和。准中性区中的最大电流出现在耗尽区的两侧。

直流电阻（静态电阻）

PN 结二极管的直流电阻或静态电阻定义了当直流电源连接到二极管时的电阻特性。如果向包含半导体二极管的电路施加外部直流电压，将在PN 结二极管特性曲线上得到一个Q点（或工作点），该点不会随时间改变。

曲线膝点及其以下的静态电阻将远大于特性曲线垂直上升部分的电阻值。通过二极管的电流越小，直流电阻越大。

$R_{DC} = \frac{V_{DC}}{I_{DC}}$

交流电阻（动态电阻）

动态电阻来源于肖克莱二极管方程。它定义了当交流电源连接到二极管时的电阻特性，这取决于PN 结二极管的直流偏置。

如果向包含二极管的电路施加外部正弦信号，变化的输入将使瞬时Q点在特性曲线上略微偏离当前位置，从而定义了电压和电流的确定变化。

当没有外部交流信号施加时，工作点将是Q点（或静态点），由施加的直流信号电平决定。通过降低工作点的Q值，二极管的交流电阻增加。简而言之，它相当于PN 二极管电压-电流曲线的斜率。

$r_d = \frac{\Delta V_d}{\Delta I_d}$

平均交流电阻

如果输入信号足够大以产生较大的摆动，则该区域与二极管相关的电阻称为平均交流电阻。它由连接外部输入电压最小值和最大值交点的直线决定。

$R_{avg} = \frac{\Delta V_d}{\Delta I_d} \quad (\text{峰-峰})$

过渡电容

过渡电容也可以称为耗尽层电容或空间电荷电容。它主要出现在反向偏置配置中，其中P型和N型区域具有较低的电阻，而耗尽层可能充当电介质。

这种电容是由于外部电压的变化导致耗尽层边缘的固定电荷发生变化。它取决于耗尽层的介电常数和宽度。如果耗尽层宽度增加，过渡电容减小。

$C_T = \frac{\varepsilon_s}{w} = \sqrt{\frac{q\varepsilon_s}{2(\phi_i - V_D)} \cdot \frac{N_a N_d}{(N_a + N_d)}}$

扩散电容

扩散电容也可以称为存储电容，主要出现在正向偏置配置中。它是由于二极管两端（即PN 结二极管正向偏置配置中的阳极到阴极）之间载流子的传输而产生的电容。

如果允许电流通过半导体器件，将在某个时间点在器件中产生一些电荷。如果施加的外部电压和电流发生变化，将在传输中产生不同数量的电荷。

传输电荷与电压微分变化的比值即为扩散电容。如果电流水平增加，则扩散电容水平自动增加。

电流水平的增加将导致相关电阻和时间常数的降低，这在高速应用中非常重要。扩散电容值远大于过渡电容值，并且与直流电流值成正比。

$C_{\text{diff}} = \frac{dQ}{dV} = \left[\frac{dI(V)}{dV}\right] \Gamma_F$

存储时间

PN 结二极管在正向偏置配置中表现为完美导体，在反向偏置配置中表现为完美绝缘体。在从正向偏置切换到反向偏置时，电流流动保持恒定水平。电流反转并保持恒定水平的时间称为存储时间（Ts）。

电子从P型返回N型以及空穴从N型返回P型所需的时间即为存储时间。这个值可以通过PN 结的几何结构来确定。在此存储时间内，二极管表现为短路。

过渡时间

电流在保持恒定水平后降低到反向漏电流值所需的时间称为过渡时间。过渡时间值由PN 结的几何结构和P型与N型材料的掺杂浓度决定。

反向恢复时间

反向恢复时间是存储时间和过渡时间的总和。它是二极管从反向漏电流将施加的电流信号提升到稳态值的10%所需的时间。PN 结二极管的反向恢复时间通常在微秒量级。

对于广泛使用的1N4148小信号整流二极管，其反向恢复时间通常为4纳秒，而对于通用整流二极管，其反向恢复时间为2微秒。通过较高的反向漏电流和较高的正向电压降，可以实现快速的开关速度。反向恢复时间用 $T_{rr}$ 表示。

数据手册分析

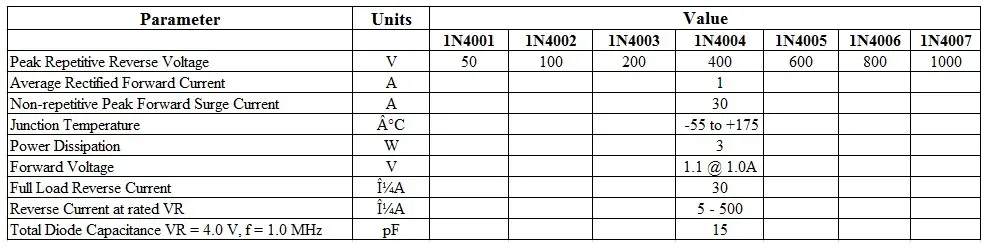
总结

本文简要介绍了不同的二极管特性，包括反向恢复时间。这些特性对于理解二极管在电路中的行为以及选择适合特定应用的二极管非常重要。